Homepage

European Microscopy Congress 2020 Abstract Database

Wave-optical properties and spatial resolution in point-projection microscopy and holography

Wave-optical properties and spatial resolution in point-projection microscopy and holography

Session

PST.1 - Phase Microscopy

Authors

Dr Faruk Krecinic (1), Dr Ralph Ernstorfer (1)

Affiliations

1. Fritz Haber Institute of the Max Planck Society

Keywords

electron wave-optics

field emission source

in-line holography

point-projection microscopy

Abstract text

Point-projection microscopy is a low-energy (typically <200 eV) electron imaging technique that uses a sharp metallic tip as a point source of electrons to project a magnified image of a sample, without any additional electron-optical lens elements. The image magnification is simply given by the geometric ratio between the sample-detector and the tip-sample distance, i.e. M=d_t-d/d_s-d. The use of field-emission sources that produce highly coherent electron beams has lead to the development of low-energy electron holography (LEEH), where at sufficiently large magnification the projected image becomes an in-line hologram that can be inverted to retrieve the real-space image of the object [1-3]. 

Although some early publications investigated the possibility of atomic scale spatial imaging with LEEH [4, 5], so far the best reported spatial resolution is 7 to 8 Å [6], where the lack of atomic resolution was mainly attributed to environmental mechanical vibrations. However, classical wave optical studies on the effect of (partial) coherence on the spatial resolution showed that increasing the size of a fully coherent source proportionally reduces the the numerical aperture and limits the spatial resolution [7, 8]. This conclusion is at odds with the observation by Cho et al [9] that showed an increase in the opening angle at which fringes are visible when the emitter is cooled, increasing the spatial coherence length. A shortcoming of the classical wave optical treatments that could explain this discrepancy is the omission of electron emission and propagation effects. Ray-tracing simulations are therefore necessary to estimate the effects of e.g. the initial electron momentum distribution [10], electron-optical aberrations, and the emission intensity distribution [11] on the spatial resolution. However, in this case it is challenging, especially when dealing with a partially coherent and spatially extended source, to relate the classical electron trajectories in a straightforward and consistent way to the electron wave function required to simulate holographic image formation.

Here we introduce a semi-classical model for a physically consistent treatment of wave-mechanical and geometric electron-optical properties of field-emission electron sources. We use it to investigate the spatial resolution limits in low-energy electron holography (LEEH), where the aberration and coherence properties of the electron source are crucial and interrelated. In the semi-classical approximation the wave function can be expressed as

 Ψ(r) = G(r) exp[iS(r)]

where G(r) is the amplitude function, and S(r) is the phase function [12, 13]. The quantum mechanical phase S for a single classical electron trajectory ending at point r is given by 

S(r) = ∫^t(r) [2K(τ)]^1/2 dτ

where K is the kinetic energy of the classical particle and the line integral is along the classical path, which is parametrized by the time τ with the upper limit of the integral given by the time of arrival t at r. The amplitude function G is determined from the initial electron momentum distribution, the spatial coherence length at the emitter, and the conservation of flux, i.e. the spread of the wave function during propagation. Summing the quantum mechanical phases and amplitudes for a complete set of classical electron trajectories arriving at point r we obtain the quantum mechanical wave function at that point, e.g. at the sample plane.

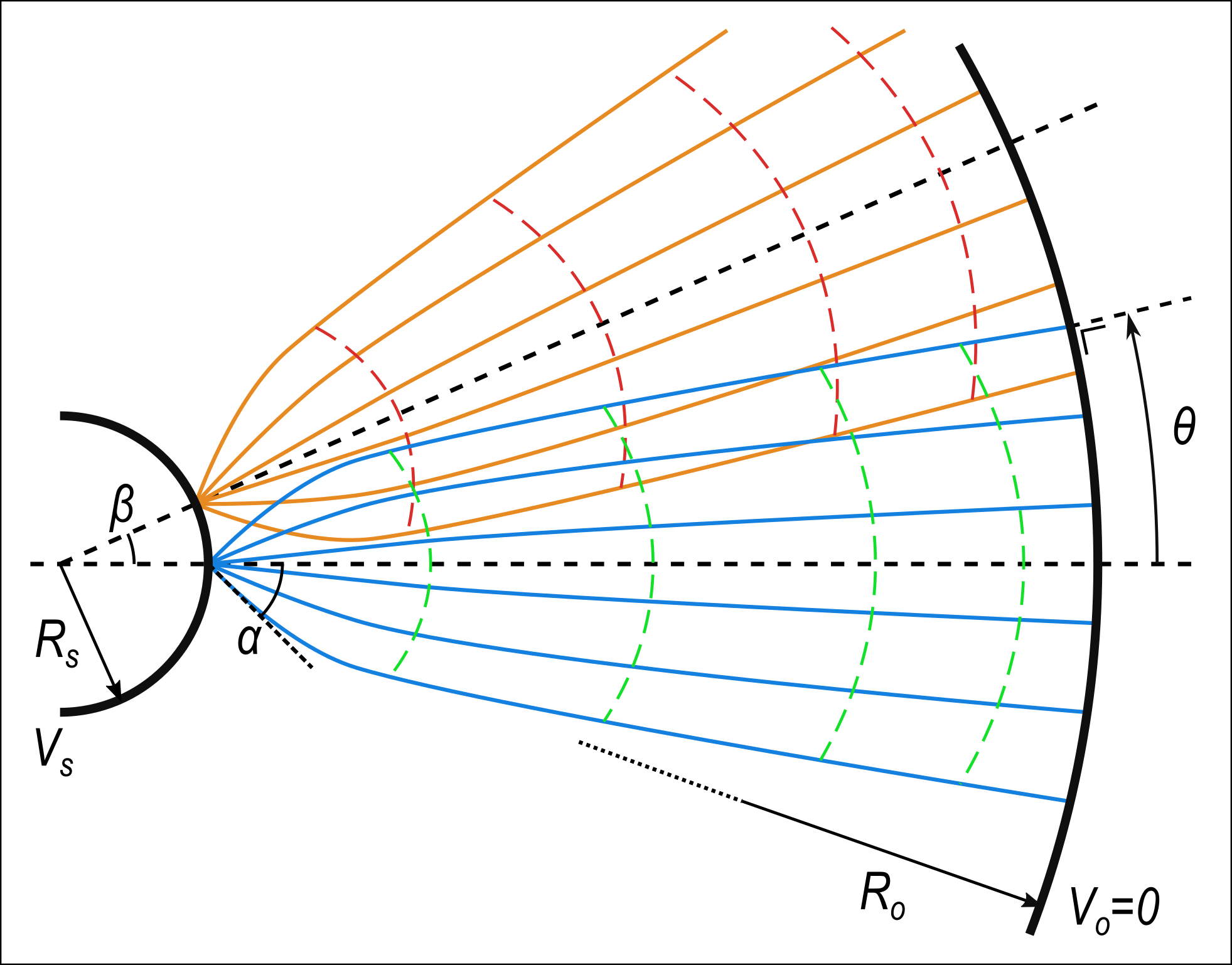
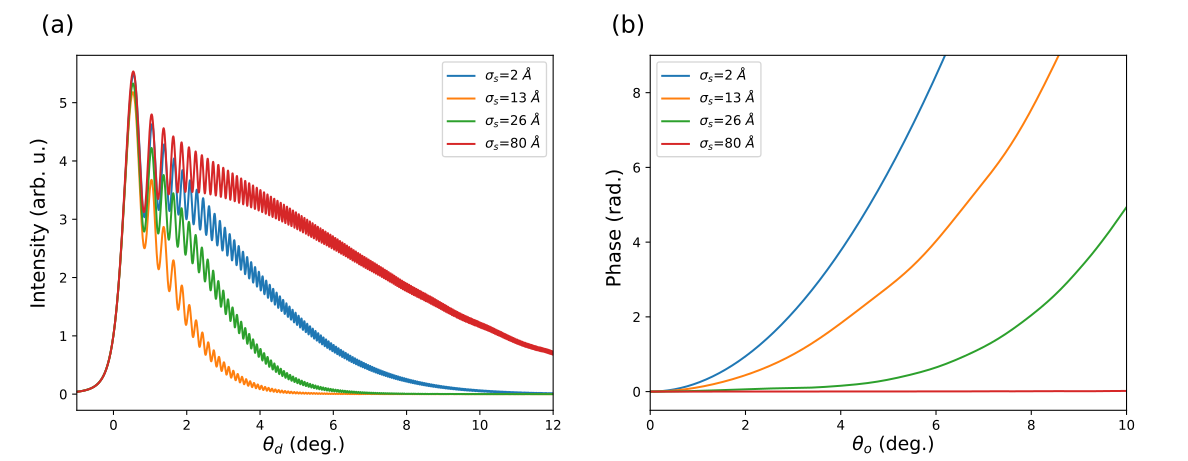
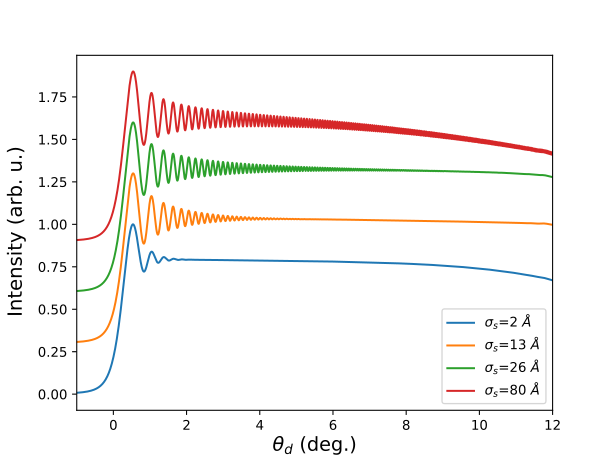
We numerically model, using the semi-classical approximation, in-line hologram formation in LEEH with a concentric spherical electrode model illustrated schematically in Fig. 1. This model captures the essential electron-optical characteristics of the problem while remaining relatively simple and transparent. We investigate the influence of four factors: (i) the spatial coherence length, (ii) partially coherent emission from an extended surface, (iii) the geometry of the cathode, and (iv) electron-optical aberrations effects. For fully coherent emission from the source surface we show that the source surface curvature can effectively counteract the reduction in numerical aperture indicated by classical wave-mechanical models, see Fig. 2(a). Nevertheless, the acceleration of electrons in the electrostatic field also clearly leads to aberrations in the phase of the wave function, see Fig. 2(b). The non-spherical wave front aberration is more pronounced for smaller coherent emitters, since coherent emitters with a spatial extent on the order of the cathode radius have initially a wave function that conforms more closely to the spherical source surface. Partially coherent emission is modeled by incoherently summing the emission from all fully coherent sub-patches of the emitting surface, where the size of the sub-patches is determined by the spatial coherence length at the source. Since wave front aberration is less pronounced for larger coherent emitters, the model shows that holographic interference fringe visibility of the partially coherent projection images is increasing proportionally to the spatial coherence length, see Fig. 3, which is indeed consistent with the experimental observations by Cho et al [9].

The semi-classical model introduced here provides a general framework to investigate and simulate partially coherent electron sources and evaluate the effect of the spatial coherence length, source geometry and electron-optical aberrations on the emitted electron beam.

Figure 1. Schematic illustration of the semi-classical concentric sphere model. The classical trajectories (blue/orange solid lines) originating from each point source emitter are normal to equiphase surfaces (green/red dashed lines) of the corresponding semi-classical wave function. The semi-classical electron wave function at any point on the object surface (R_o) is the sum of all incoming trajectories at that point.

Figure 2. Semi-classical simulation of an in-line hologram of a perfect edge on the object surface projected by the concentric spherical electrode model with R_s=50 nm,  R_o=1 μm and V_s=100 V. The wave function magnitude (a) and phase (b) are shown for varying coherent emitter sizes ranging from an atomic emitter, i.e. σ_s=2 Å, up to a spatially extended emitter of 80 Å.

Figure 3. Semi-classical simulation of the projection image from a partially coherent emitter for a range of coherence lengths of 2 to 80 Å. The electron emission from the spherical cathode surface is taken to be uniform over a spatial extent much larger than the coherence length.

References

[1] H W Fink, et al, Phys. Rev. Lett. 65, 1204 (1990).

[2] V T Binh, N. Garcia, and S. Purcell, in Advances in Imaging and Electron Physics, Vol. 95 (Academic Press, 1996) pp. 63–153.

[3] J Spence, W Qian, and A Melmed, Ultramicroscopy 52, 473 (1993).

[4] H J Kreuzer, et al, Ultramicroscopy 45, 381 (1992).

[5] H-W Fink, et al, Physical Review Letters 67, 1543 (1991).

[6] J-N Longchamp, et al, Proceedings of the National Academy of Sciences 114, 1474 (2017).

[7] P A Serena, et al, Journal of Microscopy 152, 43 (1988).

[8] T Latychevskaia, Ultramicroscopy 175, 121 (2017).

[9] B Cho, et al, Physical Review Letters 92, 246103 (2004).

[10] G Stevens, Journal of Microscopy 235, 9 (2009).

[11] M R Scheinfein, W Qian, and J Spence, Journal of Applied Physics 73, 2057 (1993).

[12] P W Hawkes and E Kasper, Principles of electron optics – Wave optics, Vol. 3 (Academic Press, 1996).

[13] Z H Huang, et al, Physical Review A 41, 32 (1990).